Updated 7 August 2023 (c) 2023
Introduction
Many of us, while still in grade school, learned about the staggering distances to planets, stars and galaxies. The sun is approximately 150 million km or 93 million miles away, a distance that is known as the “astronomical unit” (AU). Venus, our closest neighbor, is 0.72 AU from the sun, while Mars is 1.52 AU from the sun. Neptune, the most distant planet, is 30 AU from the sun (i.e., 44.8 billion km or 27.9 billion miles). The Voyager 2 spacecraft, launched in 1977, reached Jupiter just two years later, but did not reach Neptune until 1989.
The nearest stars, the triplet Alpha Centauri A, Alpha Centauri B and Proxima Centauri, are roughly 1000 times more distant, approximately 40.7 trillion km (25.3 trillion mi). Such huge distances are often given in terms of light-years, namely the distance that light travels in a Julian year of 365.25 days (9.461 trillion km or 5.879 trillion mi). Thus the Alpha/Proxima Centauri star system is roughly 4.3 light-years away. The Milky Way galaxy consists of some 300 billion stars in a spiral-shaped conglomerate roughly 100,000 light-years across.
The nearest spiral galaxy is the Andromeda Galaxy, which can be seen with many home telescopes. It is roughly 2.54 million light-years away. There are hundreds of billions of galaxies in the observable universe. As of the present date, the most distant observed galaxy is some 13.2 billion light-years away, which is more than 5000 times more distant than the Andromeda Galaxy. The age of the universe itself is currently estimated to be 13.75 billion years (plus or minus 0.011 billion years), so this galaxy must have formed soon after the big bang. An interesting online tool, which one can use to determine first-hand the age of the universe from known data, is available at [WMAP2009].
The scope of the universe is perhaps best illustrated by an example given by Australian astrophysicist Geraint Lewis. He noted that if the entire Milky Way galaxy is represented by a small coin, roughly one cm across, then the Andromeda galaxy would be another small coin roughly 25 cm (10 in) away. The observable universe would then extend for 5 km (3 mi) in every direction, encompassing some 300 billion galaxies (and roughly 3 x 1022 individual stars). And yet most of the universe is empty space! [Lewis2011].
So how are these distances measured? How can scientists possibly measure or calculate these enormous distances with any confidence?
Parallax
The most basic technique is known as parallax, which was first used by German astronomer Friedrich Wilhelm Bessel in 1838. Parallax is not sophisticated — in fact your eyes use parallax to produce the perception of 3-D vision. If you cover one eye and note the position of a nearby object, compared with more distant objects, the nearby object “moves” when you view it with the other eye. This is parallax.
The same principle is used in astronomy, where instead of using the distance between your two eyes as a baseline, researchers use the diameter of the earth’s orbit around the sun, which is 2 AU or approximately 300 million km (186 million mi). As the earth travels around the sun in its orbit, relatively close stars are observed to move slightly, with respect to other “fixed” stars that are evidently much more distant. In most cases, this movement is very slight, only a fraction of a second of arc, but reasonably accurate distance measurements can nonetheless be made for stars up to about 10,000 light-years away, encompassing over 100,000,000 stars. This scheme, which relies on very basic geometry and trigonometry, is illustrated by the following diagram [courtesy Wikimedia]:
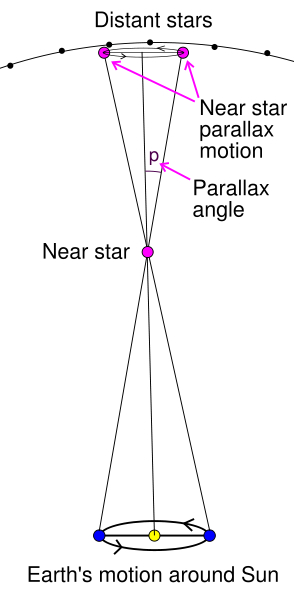
It can easily be seen, using basic trigonometry (try it!), provided p is small (which it is for all stars), that the distance D to the near star is given by 206265 AU / p, where AU is the astronomical unit mentioned above (i.e., the distance from the earth to the sun, 150 million km or 93 million miles), and p is the parallax angle measured in seconds of arc. The resulting value D when p = 1 is a unit of distance known as a parsec, which is equivalent to 3.261 light-years (i.e., 3.085 x 1013 km or 1.879 x 1013 miles).
A closely related scheme is known as expansion parallax. Here scientists study, say, the expanding cloud ring surrounding an object such as the Crab Nebula, which is the aftermath of a supernova explosion recorded by Chinese and Arab astronomers in 1054 CE. By comparing the measured rate of angular expansion with the velocity measured by the Doppler effect [Doppler2011], the distance to the object can be calculated.
It is interesting that even such a basic form of scientific reckoning as parallax is not immune to improvement. In April 2014, researchers at the NASA Goddard Space Flight Center announced that they have utilized the Hubble Space Telescope and a technique known as “spatial scanning” to greatly extend the range at which parallax measurements can be made. Using this technique, they have been able to measure parallax angles as small as five billionths of a degree, which permits measurements of distances to stars more than 75,000 light-years away (encompassing much of the Milky Way galaxy) [SD2014a].
Standard candles
For more distant objects such as galaxies, parallax measurements cannot be used because the angular motion as the earth orbits the sun is much too small to be measured even with the best telescopes. Instead, astronomers rely on what are known as “standard candles” — bright objects that, from other analyses, are known to have a fixed absolute luminosity (brightness). Since, according to elementary geometry, light flux falls off as the square of the distance, by measuring the actual brightness observed on earth using a powerful telescope, astronomers can calculate the distance to the object. If that object is, say, an object in a distant galaxy, then this serves as an approximate measurement of the distance to that galaxy.
One type of “standard candle,” which has been used since the 1920s, is the class of Cepheid variable stars (stars that periodically vary in brightness), for which there is a known relation between the period and its absolute luminosity. There are some difficulties with such measurements, but most of the issues have now been worked out satisfactorily, and distances determined using this scheme are believed accurate to within about 7% for more nearby galaxies, and 15-20% for the most distant galaxies.
Type Ia Supernovas
In recent years the most widely used standard candles are what are known as Type Ia supernovas. These occur in a binary star system when a white dwarf star starts to attract matter from a larger red dwarf star. As the white dwarf gains more and more matter, eventually the star becomes unstable and undergoes a runaway nuclear fusion reaction, producing an extremely bright event that often may briefly outshine the entire galaxy that the supernova is located in. Because this process is well understood, and can occur only within a very narrow range of total mass, the absolute luminosity Type Ia supernovas is very predictable, varying only slightly according to the shape of the supernova’s rise-fall curve.
In August 2011, worldwide attention was focused on a Type Ia supernova that exploded in the Pinwheel Galaxy (known as M101), a beautiful spiral galaxy located just above the handle of the Big Dipper in the Northern Hemisphere. This is the closest supernova to the earth since the 1987 supernova, which was visible mainly in the Southern Hemisphere. Three photos of the 2011 supernova, taken on 22, 23 and 24 Aug 2011 (just before detection, first detection, and one day later), are shown here [courtesy Peter Nugent of LBNL]:

At the present time, Type Ia supernovas are widely considered to be the most reliable “standard candle” for astronomical distance measurements. They have been used to measure distances to galaxies as far away as 13.2 billion years. The uncertainty in these measurements is typically 5%.
Type Ia supernovas have more than merely academic interest, because they have been the principal tool used during the past 13 years to deduce the startling conclusion that the universe is not only expanding, but accelerating. This was first discovered by two teams of scientists in 1998, one led by Saul Perlmutter of Lawrence Berkeley National Laboratory, and the other led by Brian P. Schmidt of Harvard University (now at Australian National University). Each team relied on measurements of Type Ia supernovas to reach their conclusion. In October 2011, Perlmutter, Schmidt and Adam Riess (a co-worker of Schmidt) were awarded the 2011 Nobel Prize in Physics [Overbye2011c].
The cosmic distance ladder
These and other techniques for astronomical measurements, collectively known as the “cosmic distance ladder,” are described in an excellent Wikipedia article [Ladder2011].
One advantage of the numerous distance-measuring schemes in use, which overlap over a range of distances from nearby to very distant, is that astronomers can calibrate and corroborate their measurements with multiple approaches. Such calibrations and corroborations thus lend an additional measure of reliability to these schemes. Indeed, by comparing results using different methods, weaknesses have been identified in certain schemes. In most cases, additional studies have demonstrated ways to guard against and correct for known difficulties.
As a single example of these multiple approaches, prior to 2011 the distance to the Pinwheel Galaxy (shown above) was determined, based on measurements of Cepheid variable stars in the galaxy, to be 20.9 million light-years, with an uncertainty of 1.8 million light-years. As of September 2011, measurements of the light output of the 2011 Type Ia supernova in the Pinwheel Galaxy are completely consistent with this distance figure.
Summary
In short, distances to astronomical objects can be and have been measured with substantial accuracy and reliability. For the most part, the calculations involved employ only basic mathematics taught in high school. Thus the overall conclusion of a universe consisting of billions of galaxies, most of them many millions of light-years away, is beyond reasonable doubt at the present time.
However, these distance figures cause insuperable problems for creationists and others who insist that the earth and the universe about us can be no older than 6000 years or so. Some of these writers, such as Henry Morris, have gone so far as to theorize that the Creator deliberately placed quadrillions of photons in space enroute to earth, with patterns strongly suggestive to 20th and 21st century astronomers that events such as supernova explosions occurred millions of years ago, when they really didn’t [Boardman1973, pg. 26]:
[T]he light rays … must have been created carrying information descriptive of historical physical events (such as super novae) which never actually occurred, because we would now be observing light rays which were created in transit and never were radiated from the stars which they seem to image.
Needless to say, even many religious believers have difficulty swallowing this “God the Great Deceiver” theology. Kenneth Miller of Brown University, for example, blasted this notion in these terms [Miller1999, pg. 80]:
What saddens me is the view of the Creator that [creationists’] intellectual contortions force them to hold. In order to defend God against the challenge they see from evolution, they have to make him into a schemer, a trickster, even a charlatan. Their version of God is one who intentionally plants misleading clues beneath our feet and in the heavens themselves. Their version of God is one who has filled the universe with so much bogus evidence that the tools of science can give us nothing more than a phony version of reality. In other words, their God has negated science by rigging the universe with fiction and deception. To embrace that God, we must reject science and worship deception itself.